In dit artikel leggen we in detail uit hoe een regressieanalyse kan worden uitgevoerd met SPSS, hoe een regressie-analyse werkt, en hoe de resultaten geïnterpreteerd en gerapporteerd kunnen worden.
We nemen hierbij ‘huizenprijzen’ als voorbeeld aan de hand waarvan we regressieanalyse (met SPSS) uitleggen.

Wanneer kies je voor een regressieanalyse?
Een regressieanalyse wordt gebruikt om het verband tussen één afhankelijke variabele (Y), en één of meerdere onafhankelijke variabelen (X) te onderzoeken. Wanneer men de invloed van één onafhankelijke variabele op Y onderzoekt spreken we van enkelvoudige lineaire regressie (ELR), en wanneer we meerdere onafhankelijke variabelen beschouwen spreken we van meervoudige lineaire regressie (MLR). Bij lineaire regressie moet de afhankelijke variabele een schaalvariabele (interval of ratio) zijn, en kunnen de onafhankelijke variabelen zowel continu zijn (e.g. numerieke variabelen zoals bijvoorbeeld leeftijd) als discreet (e.g. nominale variabelen zoals geslacht, of ordinale variabelen zoals opleidingsniveau).
Wat is de link tussen regressie, t-test en ANOVA?
In dit artikel wordt het onderscheid tussen de t-test, ANOVA en regressieanalyse besproken. Het verschil tussen deze analysemethoden heeft voornamelijk te maken met wat je wil analyseren en hoe de resultaten geïnterpreteerd kunnen worden. In essentie zijn deze drie methoden echter allemaal afgeleid van hetzelfde framework: het algemene lineaire model (the general linear model). Zo kan een t-test geïnterpreteerd worden als een enkelvoudig lineair regressiemodel waarbij de onafhankelijke variabele (X) slechts twee waarden kan aannemen (i.e. een categorische variabele die bestaat uit twee groepen, zie dummyvariabelen), en een ANOVA als een regressiemodel met meerdere onafhankelijke categorische variabelen. Om deze reden komt regressie vaker voor in wetenschappelijk onderzoek dan alleenstaande t-testen of ANOVA’s. Dit artikel focust echter op gewone lineaire regressie, en niet op de speciale gevallen t-test en ANOVA.
Modelspecificatie bij regressieanalyse
Voordat de regressieanalyse kan worden uitgevoerd in SPSS moet het regressiemodel gespecificeerd worden. Dit model drukt het verband dat je wil analyseren uit in de vorm van een vergelijking. Hierbij wordt de afhankelijke variabele (Y) als een functie van de onafhankelijke variabelen (X’en) uitgedrukt:
y = \beta_0 + \beta_1 X_1 + \beta_2 X_2 + \dots + \beta_k X_k + \epsilon
Voorbeeld: onderzoekers willen weten welke factoren de huizenprijzen in een bepaalde wijk beïnvloeden. Hiervoor werd data verzameld over 72 huizen, bestaande uit 15 verschillende variabelen. Deze variabelen zijn onder andere: de prijs, de bewoonbare ruimte in vierkante meter, het aantal slaapkamers, het type bebouwing, etc. De onderzoekers vermoeden dat de prijs van de huizen voornamelijk afhangt van drie variabelen: de bewoonbare ruimte, het aantal slaapkamers en de mobiscore van het huis. Het regressiemodel kan dan als volgt worden uitgedrukt:
\mathrm{Prijs} = \beta_0 + \beta_1 \mathrm{Ruimte} + \beta_2 \mathrm{Aantalslaapkamers} + \beta_3 \mathrm{Mobiscore} + \epsilonHierbij zijn de beta’s de coëfficiënten van het model. ?_0 wordt het y-intercept genoemd, en ?_1 tot en met ?_k (?_3 in dit geval) zijn de hellingen (slopes) van het model. Deze hellingen geven weer welke invloed elke onafhankelijke variabele heeft op de prijs van het huis.
Deze coëfficiënten of parameters geven de échte verbanden tussen de onafhankelijke en afhankelijke variabelen in de populatie weer, en zijn onbekend voor ons. We willen ze echter op basis van de beschikbare steekproef schatten. Geschatte regressiecoëfficiënten worden aangeduid met een hoedje “^”. Het geschatte regressiemodel ziet er dus als volgt uit:
\hat{\mathrm{Prijs}} = \hat{\beta_0} + \hat{\beta_1} \mathrm{Ruimte} + \hat{\beta_2} \mathrm{Aantalslaapkamers} + \hat{\beta_3} \mathrm{Mobiscore}Schatten van het regressiemodel
Het regressiemodel schatten betekent dat SPSS de coëfficiënten zal berekenen op basis van de beschikbare data. Dit kan worden gedaan door te klikken op Regression > Linear.
Onder het veld ‘Dependent’ plaats je de afhankelijke variabele, ‘vraagprijs’ in dit voorbeeld. Onder ‘Independent(s)’ komen de onafhankelijke variabelen: ‘bewoonbare ruimte’, ‘aantal slaapkamers’, ‘mobiscore’, etc.
De knop ‘Statistics’ laat toe om bijkomende statistieken te berekenen die worden weergegeven in de SPSS output. In de meeste situaties is het voldoende om ‘Estimates’, ‘Confidence intervals’, ‘Model fit’ en ‘Descriptives’ aan te vinken.
Om de residuen van het model te analyseren klik je op ‘Save’ en vink je onder zowel ‘Predicted Values’ als onder ‘Residuals’ ‘Standardized’ aan. Dit laat toe om onder de knop ‘Plots’ te specificeren dat het residuendiagram getoond moet worden. Daarvoor plaats je ‘*ZRESID’ (de gestandaardiseerde residuen) onder Y, en ‘*ZPRED’ (de gestandaardiseerde predicties van het model) onder X. Optioneel kunnen ‘Histogram’ en ‘Normal probability plot’ aangeduid worden om de normaliteit van deze residuen na te gaan. Onder de knoppen ‘Options’, ‘Style’ en ‘Bootstrap’ hoef je niets aan te duiden.
Interpreteren van de regressieanalyse output
Hier bespreken we met een SPSS output voorbeeld hoe we de SPSS output van een regressieanalyse interpreteren.
Descriptive statistics: beschrijvende statistieken van de variabelen in het model
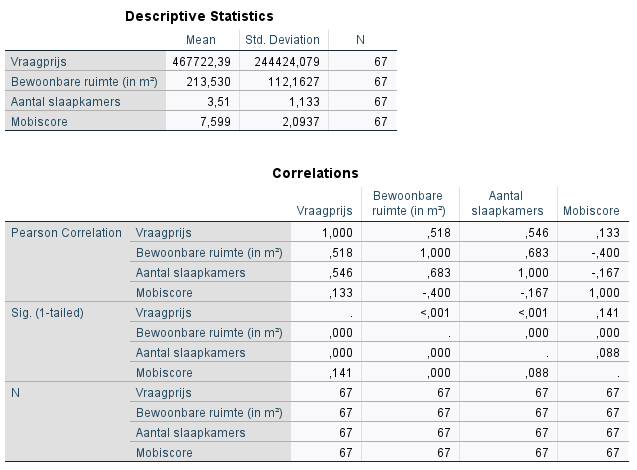

Omdat we ‘Descriptives‘ hebben aangeduid toont SPSS eerst een aantal beschrijvende statistieken van de variabelen. De tabel ‘Descriptive Statistics’ toont het gemiddelde, de standaarddeviatie en het aantal observaties voor elke variabele in het model. Daaronder worden ook de onderlingen correlaties tussen deze variabelen weergegeven.
Model summary: hoe goed ‘fit’ het model de data?


Wat echter belangrijker is is de output van de regressieanalyse. Eerst wordt de Model summary getoond. De belangrijkste statistiek in deze tabel is de R Squared ($R^2$). R squared wordt het verklarend vermogen van het model genoemd en is een maatstaf voor hoe goed het model bij de data past (i.e. de model fit). Het verklarend vermogen kan geïnterpreteerd worden als de hoeveelheid variatie in de afhankelijke variabele verklaard wordt door de onafhankelijke variabelen in het model. In dit voorbeeld wordt dus 44.9% van de variatie in huizenprijs verklaard door de drie onafhankelijke variabelen: bewoonbare ruimte, aantal slaapkamers en mobiscore.
ANOVA: de significantie van het model als geheel
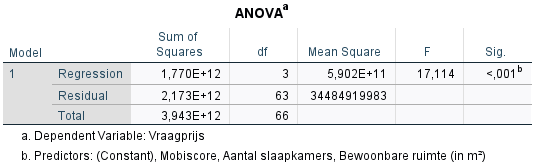

Daaronder staat de ANOVA-output. Wanneer SPSS een regressiemodel schat, voert het automatisch een ANOVA-test uit. Hierbij wordt getest of alle onafhankelijke variabelen in het model samen een significante invloed hebben op de afhankelijke variabele. De p-waarde is hier zeer significant (< 0.001), wat betekent dat minstens één van de onafhankelijke variabelen een significant invloed heeft op de huisprijs. Hieruit kan echter nog niet worden afgeleid welke variabele(n) significant verbonden zijn met de prijs.
Coefficients: de relaties tussen de afhankelijke en onafhankelijke variabelen
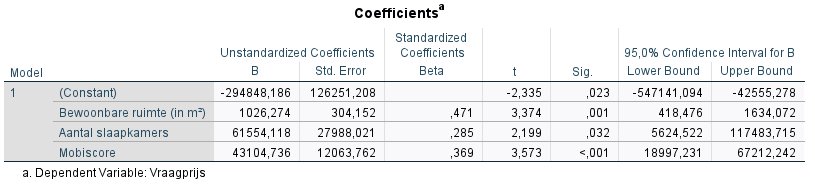

De tabel coefficients toont de geschatte coëfficiënten van het model, en of deze significant zijn of niet. In de kolom ‘Unstandardized B’ kunnen de geschatte coëfficiënten worden afgelezen. ‘Constant’ is de $\hat{\beta}_0$ coëfficiënt, en kan geïnterpreteerd worden als de gemiddelde huizenprijs wanneer alle onafhankelijke variabelen gelijk zijn aan 0. In de meeste meervoudige lineaire regressiemodellen is de interpretatie hiervan echter betekenisloos. Het bijvoorbeeld onzinnig om na te gaan wat de gemiddelde huisprijs is van huizen met een bewoonbare ruimte van 0 vierkante meter, geen slaapkamers en een mobiscore gelijk aan 0.
De coëfficiënten onder het Y-intercept hebben wél een zinvolle interpretatie. De coëfficiënt bij bewoonbare ruimte is in dit geval 1026,27. Dit betekent dat indien alle andere variabelen (slaapkamers en mobiscore) gelijk blijven, een huis dat 1 vierkante meter groter is gemiddeld €1026,27 meer zal kosten. Een regressiecoëfficiënt is dus in essentie de eerste afgeleide van de afhankelijke variabele, naar een bepaalde onafhankelijke variabele. Ze zijn dus een maatstaf voor hoe sterk de afhankelijke variabele (prijs) wijzigt, wanneer de onafhankelijke variabele wijzigt met één eenheid. Hierbij worden de andere onafhankelijke variabelen constant gehouden, wat men de ceteris paribus-conditie noemt. De geschatte coëfficiënten kunnen ingevuld worden in de vergelijking voor het model:
\hat{\mathrm{Prijs}} = -294 \ 848.19 + 1026.27 \mathrm{Ruimte} + 61 \ 554.12 \mathrm{Aantalslaapkamers} + 43 \ 104.74 \mathrm{Mobiscore}De reden waarom we naar de ongestandaardiseerde coëfficiënten kijken is omdat hun interpretatie eenvoudig is: de eenheden van de afhankelijke variabele per eenheid van de onafhankelijke variabele worden behouden (e.g. 1026 euro per vierkante meter). Het is echter moeilijk om deze ongestandaarde coëfficiënten met elkaar te vergelijken: ?_1 extra euro per vierkante meter kan moeilijk vergeleken worden met ?_2 euro per extra slaapkamer. Daarom worden de gestandaardiseerde coëfficiënten gebruikt om de ze onderling te vergelijken. In bovenstaande tabel is te zien dat, hoewel de ongestandaarde coefficient van de bewoonbare ruimte de kleinste is, deze wel de grootste gestandaardiseerde coëfficiënt heeft. Dit wil zeggen dat de bewoonbare ruimte de grootste invloed heeft op de huisprijs, en dus de belangrijkste prijspredictor is.
De kolom “Sig.” bevat de p-waarden, en geeft weer of de coëfficiënten al dan niet significant verschillen van 0. In dit voorbeeld zijn alle p-waarden kleiner dan het betrouwbaarheidsniveau 0.05, wat betekent dat alle onafhankelijke variabelen in het model een significante invloed hebben op de huizenprijzen. Dit kan worden nagegaan met de 95% betrouwbaarheidsintervallen: wanneer deze 0 niet bevatten is de coëfficiënt significant. Indien de p-waarde groter is dan 0.05, is de variabele niet significant gerelateerd aan de afhankelijke variabele. Dit wil zeggen dat, hoewel de coëfficiënt verschillend kan zijn van 0, dit verschil niet groot genoeg is om te onderscheiden of dit aan het toeval ligt of niet. Niet-significante coëfficiënten moeten ook gerapporteerd worden, en kunnen daarna eventueel verwijderd worden bij het schatten van het nieuw model. Het is echter wetenschappelijk niet integer om te testen welke variabelen significante coëfficiënten hebben, en alleen deze te behouden in het regressiemodel. Dit is namelijk p-hacking en is een aanzienlijk probleem in wetenschappelijke literatuur.
Analyse van de residuen
Tot slot kunnen de residuen of fouten van het model geanalyseerd worden. De residuen zijn het verschil tussen de geobserveerde waarden voor de afhankelijke variabele (de huisprijs) de predicties van het model voor deze afhankelijke variabele:
\epsilon_i =y_i - \hat{y}_i We hebben aangeduid dat SPSS de gestandaardiseerde residuen en de gestandaardiseerde predicties van het model moest opslaan en tonen in een spreidingsdiagram. Dit spreidingsdiagram heet het residuendiagram of de residual plot, en ziet er als volgt uit:
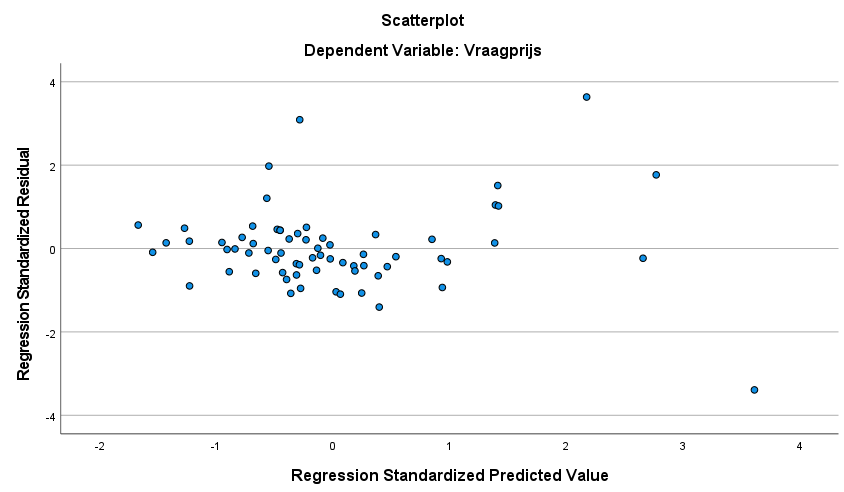

Hierbij maakt het niet veel uit of de gestandaardiseerde of ongestandaardiseerde residuen en predicties getoond worden. Wat belangrijk is is dat er geen patroon te zien is in de residuen. In een goed model zijn de residuen random, wat wil zeggen dat de predicties van het model niet consequent hoger of lager zijn dan de geobserveede waarden van de afhankelijke variabele. Bovendien willen we dat de residuen normaal verdeeld zijn rond 0, wat wil zeggen dat ze een gemiddelde waarde hebben van 0, en een constante variantie:
\epsilon \sim N (0, \sigma^2_\epsilon)
Wanneer deze residuen een constante variantie hebben, zijn ze homoskedastisch. Indien de residuen géén constante variantie hebben spreken we van heteroskedasticiteit. Dit betekent dat voor bepaalde waarden van de voorspelde afhankelijke variabele (de horizontale as op het residuendiagram), de residuen gemiddeld verder of dichter bij 0 liggen. Heteroskedastische residuen kunnen daarom vaak herkend worden aan de hand van een ‘fanning-in’ of ‘fanning-out’ patroon in het residuendiagram:
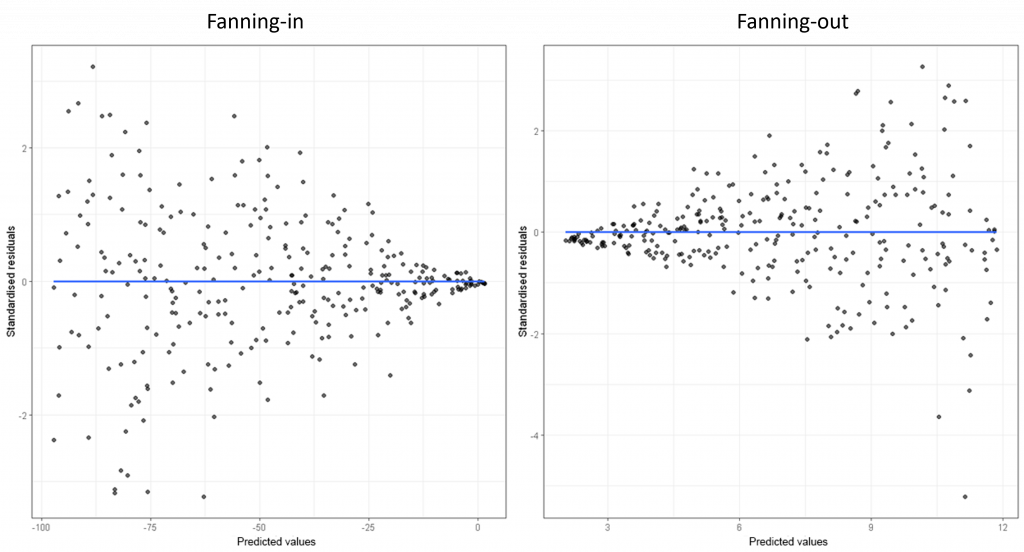

In het fanning-out patroon aan de rechterkant is te zien dat voor grotere waarden van de afhankelijke variabele, de voorspellingen van het model dus minder goed zijn: de residuen of fouten worden steeds groter. Formeel kan de aanwezigheid van heteroskedasticiteit getest worden met de White test for heteroskedasticity. Dit probleem kan ervoor zorgen dat de standaardfouten van de geschatte coëfficiënten niet meer correct zijn, waardoor de betrouwbaarheidsintervallen en hypothesetoetsen voor deze coëfficiënten misleidend kunnen zijn. Als gevolg kan een coëfficiënt bijvoorbeeld niet-significant zijn, terwijl dit in werkelijkheid wél zo is. Mogelijke strategieën om heteroskedasticiteit op te lossen zijn:
- Kijken of er belangrijke onafhankelijke variabelen niet zijn opgenomen in het model (omitted variables)
- Variabelen (vaak de afhankelijke variabele) transformeren: het natuurlijk logaritme nemen van de afhankelijke variabele en het model opnieuw schatten zorgt vaak voor een betere fit
- Robuste standaardfouten gebruiken
In het model voor de huisprijzen is geen duidelijk patroon te zien in de residuen, op één mogelijke observatie rechtsonder na. In een verdere analyse kan daarom gekozen worden om het natuurlijk logaritme van de prijs te gebruiken als afhankelijke variabele. Hoe je de resultaten het best kunt rapporteren verschilt per ‘stijl’. Lees hier meer over rapporteren resultaten regressie/ANOVA (inclusief voorbeelden in APA-stijl) . Wil je meer dan rapporteren maar wil je dit niet zelf doen, bekijk dan ook onze pagina over het laten schrijven van je scriptie, of ons artikel specifiek over scriptie-ghostwriters.
In conclusie is lineaire regressie een krachtig hulpmiddel voor het analyseren van gegevens en het verkrijgen van inzicht in de relaties tussen variabelen. Regressie kan gebruikt worden om variatie in de afhankelijke variabele te verklaren, en om waarden voor deze variabele te voorspellen.