Hoe bereken je een (95%) betrouwbaarheidsinterval voor populatie proporties?
“Confidence interval voor population proportion met unknown population standard deviation”
Stel je hebt een klanttevredenheid poll/survey gehouden waarin je vraagt hoe tevreden mensen zijn met je service of website.
Laat we veronderstellen dat daaruit is gekomen dat 70% van de mensen die je gevraagd hebt (500 mensen is de totale steekproef (‘sample’)), aangegeven heeft tevreden (of zeer tevreden) te zijn. (tevredenheid kan natuurlijk ook gedefinieerd zijn als bijv. alle antwoorden boven de 3 in een likert 5punt schaal (dit spreek je overigens uit als ‘likkert’, niet ‘laikert’). Zie het voorbeeld hieronder van een Likert-schaal voorbeeld mbt tevredenheid uit een poll/survey.)
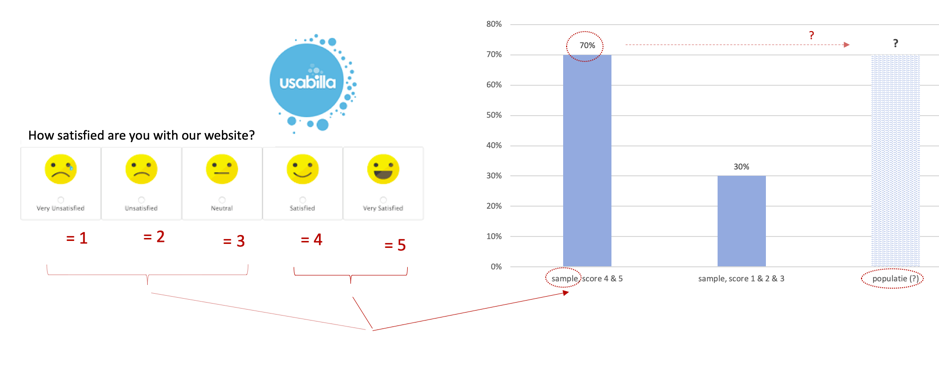
Maar hoe zeggen we nu iets over de populatie (bijv. alle website bezoekers) ipv enkel over onze sample (de subset van alle website die heeft gereageerd op onze survey)?
Eerst een sprongetje van beschrijvende statistiek naar inferentiele statistiek
De volgende vraag aan ons zal zijn ‘is deze 70% significant’? Dit is een lastige vraag maar met name omdat deze vraag een beetje onduidelijk is in deze situatie.
Deze vraag past beter bij een situatie waar je een verschil rapporteert. Bijvoorbeeld; ‘website x heeft een hoger percentage tevreden bezoekers dan website y’. Dit statement kun je op basis van je data toetsen (even verondersteld dat je dezelfde uitvraag over 2 sites hebt gedaan). Als je in dit geval na een significantie toets (bijvoorbeeld een t-toets) de p-waarde kleiner is dan .05 (dit is de kans dat het verschil tussen deze twee groepen (tevredenheid website x en website y) door toeval is ontstaan ipv door een echt effect) dan mag je het verschil (vaak ‘het effect’ genoemd) significant noemen. Wat gewoon aangeeft dat de kans 5% of kleiner is dat het verschil in tevredenheid tussen site x en site y puur toeval was.
In ons geval met ‘70% is tevreden’, wat zou significantie dan inhouden?
In een beschrijvend gegeven als dit (‘een populatie proportie’) wordt dan eigenlijk bedoeld met significantie of deze 70% uit je survey ook in de echte totale populatie 70% is. Maar dan zijn we er nog niet helemaal uit. Want…
- We zullen de echte tevredenheid van de totale populatie nooit achterhalen (tenzij we daadwerkelijke 100% van de website bezoekers zover krijgen hun tevredenheid uit te vragen. En dan hebben we eigenlijk gelijk geen significantie toets meer nodig)
- Stel dat we op magische wijze te weten komen dat voor onze ‘hoe tevreden ben je?’ (Usabilla®) uitvraag de tevreden proportie 71% zou zijn? Zou je je gevonden sample resultaat van 70% dan ‘niet significant’ noemen? Daar voel je misschien wel aan dat wel of niet significant hier niet het meest veelzeggend is.
Daarom doen we dit voor het inschatten van populatieproporties en populatie gemiddelden op basis van samples (survey data bijvoorbeeld) net even iets anders. (In dit voorbeeld gebruiken we steeds alleen populatieproporties, maar dit werkt in essentie hetzelfde voor populatie gemiddelden).
Betrouwbaarheidsintervallen to the rescue!
Werk je aan een scriptie of paper? Bekijk dan ook eens deze opties om je scriptie te laten schrijven, scriptiehulp en de opties voor scriptie ghostwriters!
Populatie proporties kunnen we informatiever maken door betrouwbaarheidsintervallen te berekenen en toe te voegen.
Een betrouwbaarheidsinterval is een ‘range‘ (een interval) waarvan we zeggen dat de gevonden waarde (in ons voorbeeld de 70%) met ‘bepaalde zekerheid’ tussen ligt. De ‘bepaalde zekerheid’. Dit is het ‘Confidence Level’. Dit is net als bij het significantie toetsen eigenlijk de ‘1 – alpha’ waarde. Hier is voor nu geen formule voor nodig, dit is eigenlijk een vrij arbitrair gekozen waarde, die verschilt per discipline afhankelijk van de ‘kosten’ van het vinden van een effect dat er niet is. (In de psychologie wordt meestal een alpha van .05 (=5%) gebruikt, terwijl in een test met medicijnen oid bijvoorbeeld .001 (0,1%) of nog lager gebruikt zal worden.)
(Voor klanttevredenheids onderzoek is het gebruikelijk een alpha van .05 (5%) te hanteren)
Laten we als confidence level ‘95%’ nemen ( = een alpha van .05)
Het uiteindelijke statement (wat in essentie weer heel veel lijkt op het significant verklaren van een effect) is terug te brengen tot:
‘met 95% zekerheid kunnen we zeggen dat het tevredenheids percentage van de gehele populatie (ipv slechts de sample) ergens tussen ..% (bijvoorbeeld 65%) en …% (bijvoorbeeld 75%) ligt’.
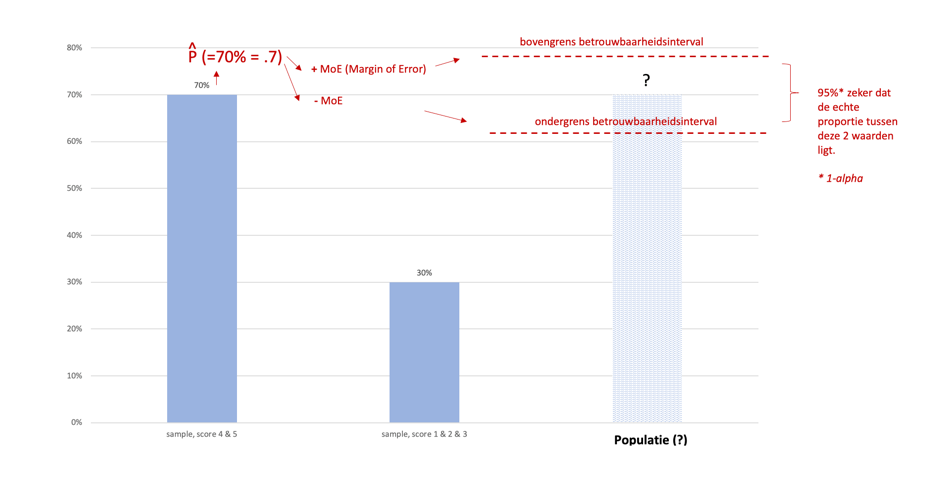

Om nu beide waarden te achterhalen (waar nu de puntjes staan), die nu vervangen zijn door de voorbeelden 65% (als ‘ondergrens’) en 75% (als ‘bovengrens’) hoeven we maar 1 waarde te berekenen.
Dit is de ‘Margin of Error’ (MoE).
De MoE (Margin of Error) is dus de afstand van onze beste gok van de ‘echte proportie’, dit is de proportie uit je survey (sample). In ons voorbeeld 70%. De MoE gaan we nu berekenen om dit van onze 70% (70% omdat dit het resultaat van onze survey is) af te trekken om de ondergrens van het betrouwbaarheidsinterval te berekenen (deze waarde is onbekend maar was 65% in ons voorbeeld). En we gaan deze MoE waarde bij onze beste gok (weer de 70% uit de survey) optellen om de bovengrens van onze betrouwbaarheidsinterval te berekenen (deze waarde is onbekend maar was 75% in ons voorbeeld).
De Margin of Error (‘MoE’) berekenen
Formule:


Om de MoE (margin of error) te berekenen hebben we nodig;
- p_hat (p^) = proportie (in ons voorbeeld is dit 70% -> .7)
- alpha = 1 – confidence level (in ons voorbeeld 1 – 95% -> .05)
- n = grootte van je steekproef. Het aantal bezoekers dat je usabilla survey heeft ingevuld (aantal regels in je dataset)
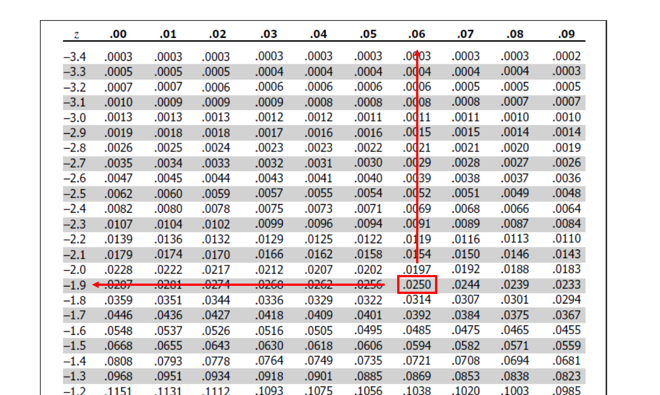
- Critical Z values. Dit kan je old-school opzoeken in een tabel. (zoek alpha/2 (=.025), pak dan de waarde links (1.9 (negeer de min)) waarde boven (0.6) er bij optellen)
-> Z(alpha/2) = 1.96

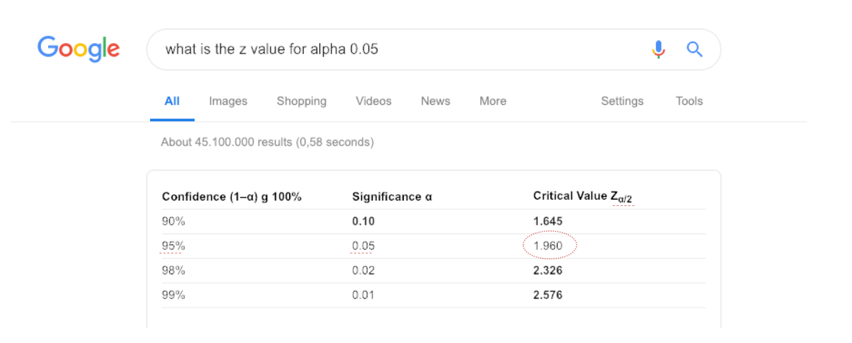
Of gewoon googlen:
(Let wel op dat alpha=.05 en je de critical Z value voor alpha/2 moet hebben)

In verband met automatiseren (bijvoorbeeld indien het herhaaldelijk berekend moet worden voor maandelijkse KPI’s) kun je het best excel gebruiken ipv een vaste waarde (voor als je je confidence level (en dus je alpha) wilt wijzigen)
Dit doe je in excel door de formule =NORM.S.INV(alpha (bijv. .05)gedeeld door twee)


Excel critical Z values. In ons voorbeeld zou dit worden =NORM.S.INV(.025) wat uitkomt op (afgerond) 1.96.
Nu heb je alle waarden die je nodig hebt. Terug naar de formule:


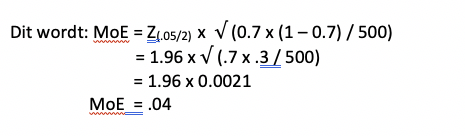
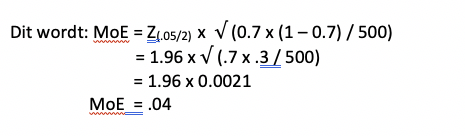
Let op, deze ‘marge’ (MoE) werkt beide kanten op. De ‘echte’ formule voor het berekenen van het betrouwbaarheidsinterval, is dan ook net iets uitgebreider dan het berekenen van de MoE.
Let op de ‘spiegeling’, hij is dus veel simpeler dan hij op het oog lijkt omdat het eigenlijk een herhaling is met het enige verschil de + en – (onder de groene pijlen).


Wat hier eigenlijk staat is simpelweg;
‘Proportie uit je sample (usabilla survey resultaat (70% is tevreden)) minus de Margin of Error is sowieso kleiner dan de echte (onbekende) tevredenheid uit populatie (ipv uit sample) (u). En dezelfde echte tevredenheid (uit de totale populatie) is sowieso kleiner dan proportie uit sample (70%) plus de Margin of Error’.
Hieronder hetzelfde maar met wat meer toelichting.
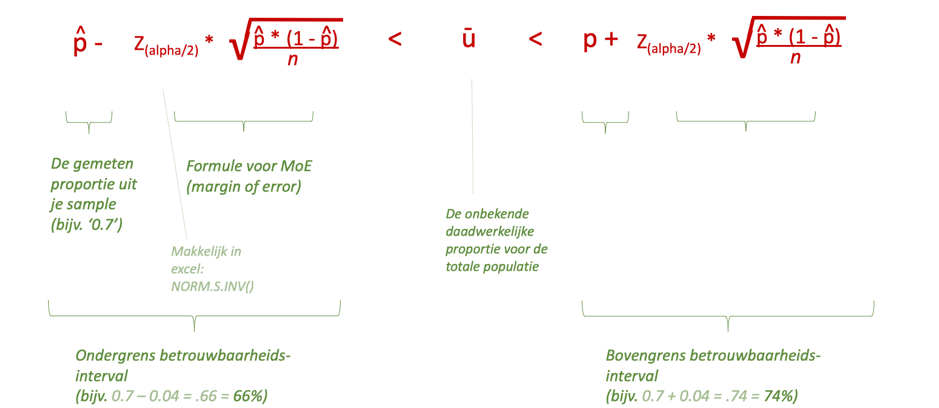

In ons voorbeeld krijgen we dan een betrouwbaarheidsinterval (met een zekerheid van 95%) van 66% tot 74%.
Want:
” 0.7 – (1.96 x √ (0.7 x 0.3 / 500)) = 0.66 ” (dus de ondergrens is 66%)
” 0.7 + (1.96 x √ (0.7 x 0.3 / 500)) = 0.74 ” (dus de bovengrens is 74%)
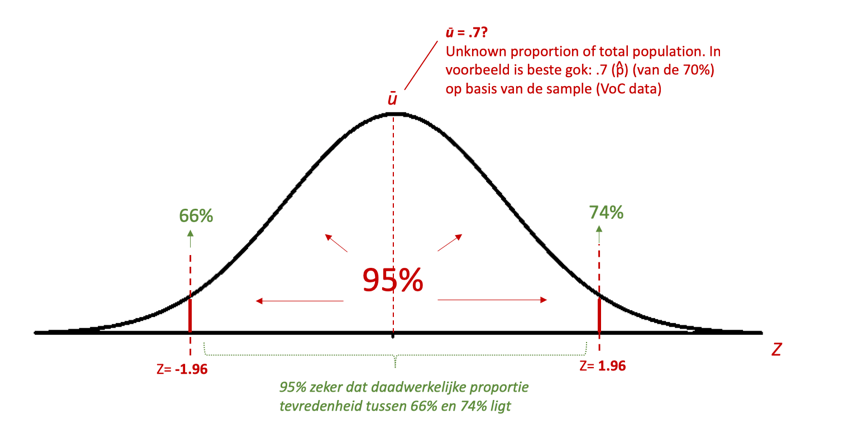

‘We kunnen met 95% zekerheid zeggen dat de daadwerkelijke proportie tevredenheid (dus over alle uwv.nl bezoekers) tussen de 66% en 74% ligt’.


Ben je je scriptie of een essay aan het schrijven? Bekijk ook eens onze andere artikelen die je kunnen helpen bij het schrijven van een scriptie of essay.